Geraden und Ebenen

Geradengleichungen

$g:\; \vec{x} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} + t \cdot \begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix},\; t \in \mathbb{R}$

$\Rightarrow\; \vec{x} = \vec{p} + t \cdot \vec{d}$

Dabei ist \(\vec{p}\) der Ortsvektor zu einem Punkt \(P\) auf der Geraden (dem Aufpunkt) und \(\vec{d}\) der Richtungsvektor, der auf der Geraden verläuft.

Visualisierung der Geradengleichung \(\vec{x} = \vec{p} + t\,\vec{v}\)

\(\vec{p}\) (rot) verschiebt die Gerade, \(\vec{v}\) (blau) gibt ihre Richtung vor.

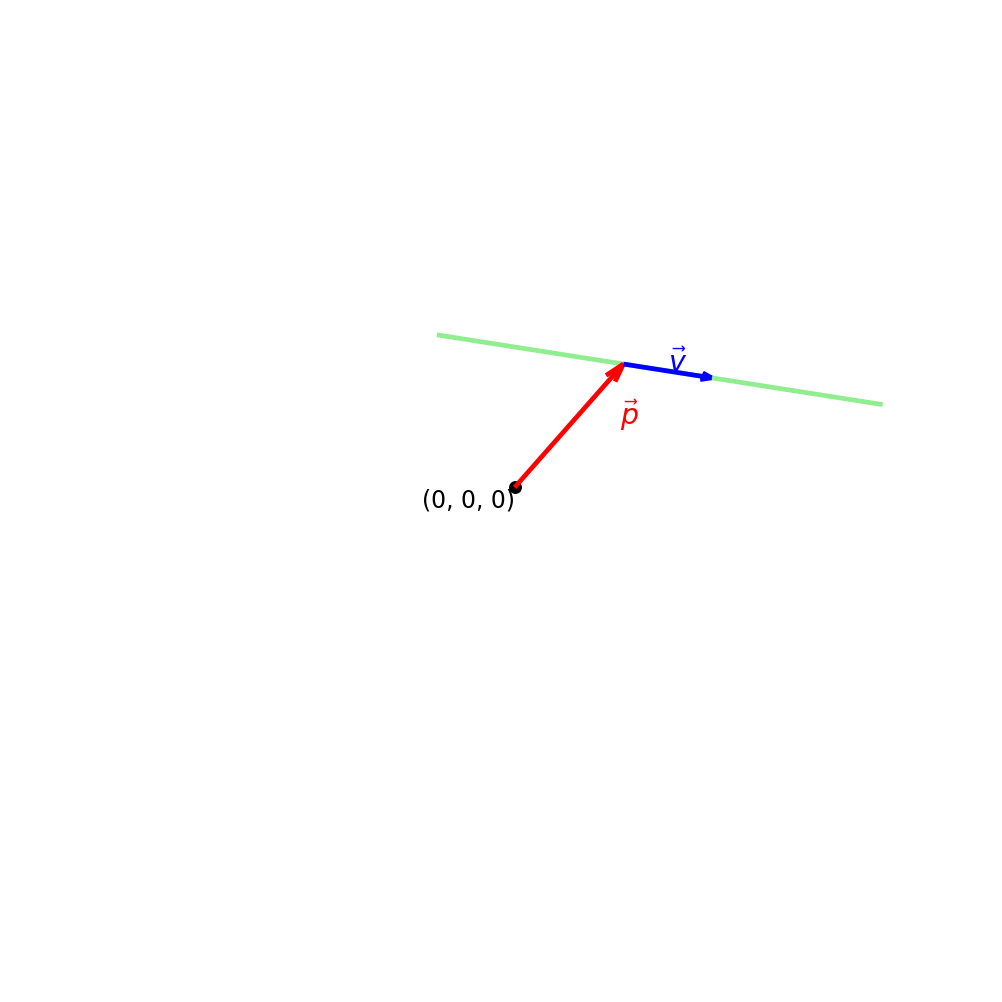
Der Parameter \(t\) bestimmt die Position auf der Geraden: \(\,\vec{X}(t) = \vec{p} + t\,\vec{v}\). Bei \(t=0\) liegt man im Aufpunkt \(\vec{p}\), bei \(t>0\) bewegt man sich in Richtung \(\vec{v}\), bei \(t<0\) entgegen der Richtung. In der Simulation kannst du \(t\) und die Definitionsmenge \([t_{\min},\,t_{\max}]\) wählen.

Wie berechnet man einen Punkt auf der Geraden?

Um einen Punkt auf der Geraden zu berechnen, wählst du einen Wert für den Parameter \(t\) und setzt ihn in die Gleichung \(\vec{x}(t) = \vec{p} + t \cdot \vec{d}\) ein.

Beispiel:

Gegeben: \(\vec{p} = (2, -1, 4)\) und \(\vec{d} = (3, 2, -1)\)

oder in Spaltenform:

\(\vec{p} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix}, \quad \vec{d} = \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix}\)

Schritt 1: Wähle einen Parameter, z.B. \(t = 2\)

Schritt 2: Setze in die Gleichung ein:

\(\vec{x}(2) = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix}\)

Schritt 3: Multipliziere den Skalar aus:

\(2 \cdot \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix} = \begin{pmatrix} 6 \\ 4 \\ -2 \end{pmatrix}\)

Schritt 4: Addiere die Vektoren:

\(\vec{x}(2) = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix} + \begin{pmatrix} 6 \\ 4 \\ -2 \end{pmatrix} = \begin{pmatrix} 8 \\ 3 \\ 2 \end{pmatrix}\)

✓ Punkt auf der Geraden: \(P(8 \mid 3 \mid 2)\)

Punktprobe: Liegt ein Punkt auf der Geraden?

Wenn du prüfen möchtest, ob ein gegebener Punkt \(Q\) auf der Geraden liegt, setzt du seine Koordinaten in die Geradengleichung ein und schaust, ob du einen konsistenten Parameter \(t\) erhältst.

Beispiel:

Gegeben: Punkt \(Q(8 \mid 3 \mid 2)\) und Gerade \(\vec{x} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix} + t \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix}\)

Schritt 1: Setze Koordinaten gleich:

\(\begin{pmatrix} 8 \\ 3 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix} + t \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix}\)

Schritt 2: Schreibe komponentenweise auf:

\(\begin{cases} 8 = 2 + 3t \\ 3 = -1 + 2t \\ 2 = 4 - t \end{cases}\)

Schritt 3: Löse jede Gleichung nach \(t\) auf:

Aus Gleichung 1: \(8 = 2 + 3t \Rightarrow 6 = 3t \Rightarrow t = 2\)

Aus Gleichung 2: \(3 = -1 + 2t \Rightarrow 4 = 2t \Rightarrow t = 2\)

Aus Gleichung 3: \(2 = 4 - t \Rightarrow -2 = -t \Rightarrow t = 2\)

✓ Überall gleiches \(t = 2\) → Punkt \(Q\) liegt auf der Geraden!

Merksatz: Wenn aus allen drei Komponenten der gleiche Parameterwert \(t\) herauskommt, liegt der Punkt auf der Geraden. Sonst nicht!

Simulation in \(\mathbb{R}^3\)

Gib den Ortsvektor \(\vec{p} = (a_1,a_2,a_3)\), den Richtungsvektor \(\vec{d} = (u_1,u_2,u_3)\) sowie einen festen Wert \(t\) ein.

a₁ a₂ a₃ u₁ u₂ u₃ t t_min t_max

Ebenengleichungen

Parameterform

Eine Ebene kann in Parameterform dargestellt werden:

$E: \vec{x} = \vec{p} + s \cdot \vec{u} + t \cdot \vec{v}, \quad s, t \in \mathbb{R}$

$\vec{p}$ ist der Ortsvektor eines Punkts der Ebene und bestimmt die Position der Ebene im Raum (mit $\vec{p}$ verschiebst du die Ebene). $\vec{u}$ und $\vec{v}$ sind Richtungsvektoren (Spannvektoren), die die Ausrichtung und Form der Ebene bestimmen.

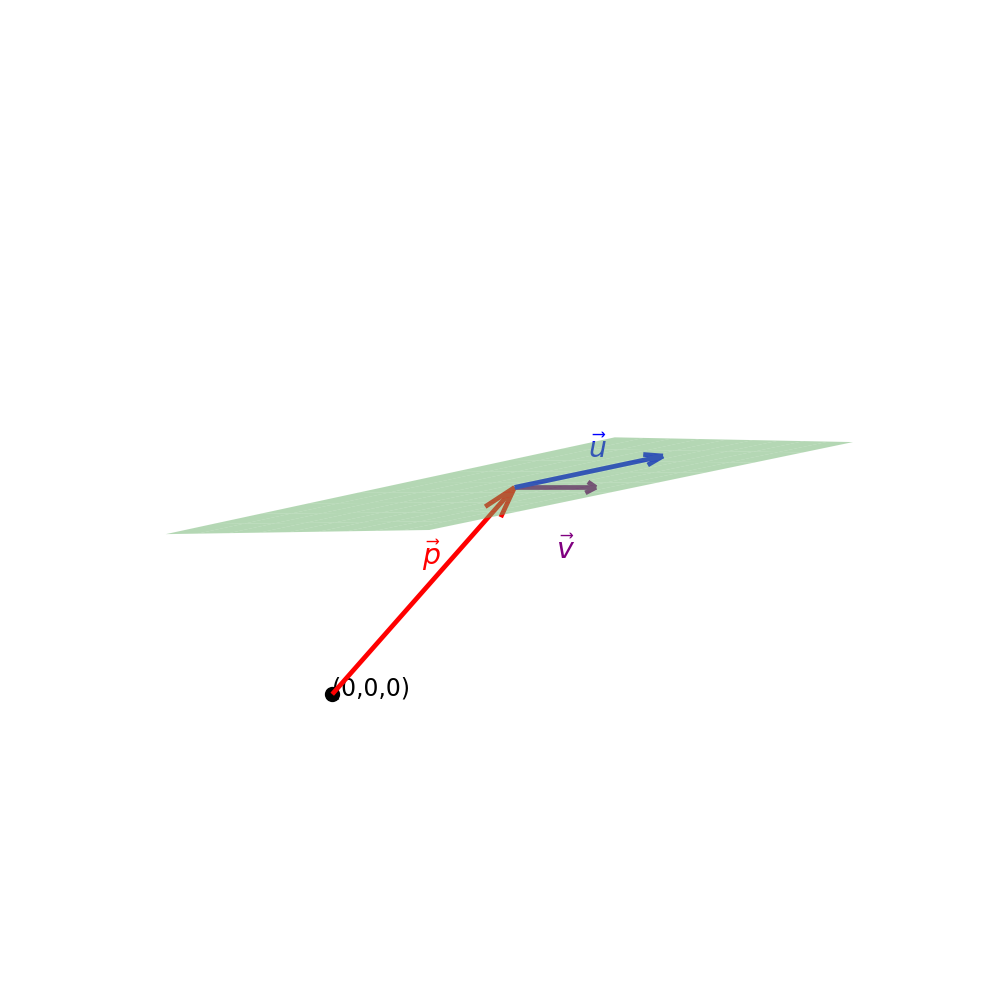
Visualisierung der Ebenengleichung \(\vec{x} = \vec{p} + s\,\vec{u} + t\,\vec{v}\)

\(\vec{p}\) (rot) verschiebt die Ebene, \(\vec{u}\) (blau) und \(\vec{v}\) (lila) spannen die Ebene auf.

Wie berechnet man einen Punkt auf der Ebene? (Rechnung)

Um einen Punkt auf der Ebene zu berechnen, wählst du Werte für die Parameter \(s\) und \(t\) und setzt sie in die Gleichung \(\vec{x}(s,t) = \vec{p} + s \cdot \vec{u} + t \cdot \vec{v}\) ein.

Beispiel:

Gegeben:

\(\vec{p} = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}, \quad \vec{u} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}, \quad \vec{v} = \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix}\)

Schritt 1: Wähle Parameter, z.B. \(s = 2\) und \(t = -1\)

Schritt 2: Setze in die Gleichung ein:

\(\vec{x}(2, -1) = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} + (-1) \cdot \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix}\)

Schritt 3: Berechne die skalaren Multiplikationen:

\(2 \cdot \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \\ 2 \end{pmatrix} \quad \text{und} \quad (-1) \cdot \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix}\)

Schritt 4: Addiere alle Vektoren:

\(\vec{x} = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 4 \\ 0 \\ 2 \end{pmatrix} + \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} = \begin{pmatrix} 6 \\ -1 \\ 0 \end{pmatrix}\)

✓ Punkt auf der Ebene: \(X(6 \mid -1 \mid 0)\)

Simulation in \(\mathbb{R}^3\) (Ebene)

Wähle Ortsvektor \(\vec{p}\), Richtungsvektoren \(\vec{u},\vec{v}\) und die Bereiche für \(s\) und \(t\).

Der Normalenvektor \(\vec{n}\) steht senkrecht auf der Ebene.

a₁ a₂ a₃ u₁ u₂ u₃ v₁ v₂ v₃ s_min s_max t_min t_max s t

Vorwissen: Normalenvektor · Skalar & Skalarprodukt

Normalenform

Die Normalenform verwendet einen Normalenvektor $\vec{n}$, der senkrecht auf der Ebene steht:

$E: \vec{n} \cdot (\vec{x} - \vec{p}) = 0$

• $\vec{n}$ – Normalenvektor: Steht senkrecht auf der Ebene. Schreibweise: $\vec{n} = \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}$.
• $\vec{p}$ – Stützvektor (Aufpunkt): Ortsvektor eines bekannten Punktes auf der Ebene, z.B. $\vec{p} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}$.
• $\vec{x}$ – Ortsvektor eines beliebigen Punktes: Beschreibt alle Punkte auf der Ebene, $\vec{x} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$.

Warum gilt $\vec{n} \cdot (\vec{x} - \vec{p}) = 0$? (geometrisch + rechnerisch)

Geometrische Idee:
Der Vektor $\vec{x} - \vec{p}$ ist der Verbindungsvektor von Punkt $\vec{p}$ zu einem beliebigen Punkt $\vec{x}$ auf der Ebene. Dieser Vektor liegt immer in der Ebene.

Da der Normalenvektor $\vec{n}$ senkrecht auf der Ebene steht, ist er auch senkrecht auf jedem Vektor, der in der Ebene liegt – also auch senkrecht auf $\vec{x} - \vec{p}$.

Das Skalarprodukt zweier senkrechter Vektoren ist immer 0:

$\vec{n} \perp (\vec{x} - \vec{p}) \quad \Rightarrow \quad \vec{n} \cdot (\vec{x} - \vec{p}) = 0$

Beispiel: Punktprobe in der Normalenform

Gegeben: Ebene $E: \vec{n} \cdot (\vec{x} - \vec{p}) = 0$ mit $\vec{n} = \begin{pmatrix} 0 \\ -27 \\ 81 \end{pmatrix}$ und $\vec{p} = \begin{pmatrix} 3 \\ 5 \\ 7 \end{pmatrix}$
Frage: Liegt der Punkt $Q(3 \mid 2 \mid 7)$ auf der Ebene?

Schritt 1: Verbindungsvektor berechnen: $$\vec{x} - \vec{p} = \begin{pmatrix} 3 \\ 2 \\ 7 \end{pmatrix} - \begin{pmatrix} 3 \\ 5 \\ 7 \end{pmatrix} = \begin{pmatrix} 0 \\ -3 \\ 0 \end{pmatrix}$$

Schritt 2: Skalarprodukt mit Normalenvektor: $$\vec{n} \cdot (\vec{x} - \vec{p}) = \begin{pmatrix} 0 \\ -27 \\ 81 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ -3 \\ 0 \end{pmatrix} = 0 \cdot 0 + (-27) \cdot (-3) + 81 \cdot 0 = 0 + 81 + 0 = 81$$

Ergebnis: Das Skalarprodukt ist 81 ≠ 0, daher liegt $Q(3, 2, 7)$ nicht auf der Ebene. ✗

Simulation in \(\mathbb{R}^3\) (Normalenform)

Wähle Normalenvektor \(\vec{n}\) und Stützvektor \(\vec{p}\).

n₁ n₂ n₃ p₁ p₂ p₃

Koordinatenform

Durch Ausmultiplizieren der Normalenform erhält man die Koordinatenform. Ausgehend von $\,\vec{n} \cdot (\vec{x} - \vec{p}) = 0\,$ mit $\,\vec{n} = \begin{pmatrix} a \\ b \\ c \end{pmatrix}\,$ und $\,\vec{p} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}\,$ gilt:

$E: ax + by + cz = d$

• a, b, c: Komponenten des Normalenvektors $\vec{n}=\begin{pmatrix} a \\ b \\ c \end{pmatrix}$; geben die Richtung senkrecht zur Ebene an.
• x, y, z: Koordinaten eines beliebigen Punktes $\vec{x}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ auf der Ebene.
• d: Ebenenkonstante; berechnet sich über das Skalarprodukt $d=\vec{n}\cdot\vec{p}=a x_0 + b y_0 + c z_0$.

Simulation in \(\mathbb{R}^3\) (Koordinatenform)

Wähle die Koeffizienten \(a,b,c\) des Normalenvektors und die Konstante \(d\).

a b c d