Kurs

Lagebeziehungen - Ebenen und Geraden

Quiz starten
Voraussetzungen: Für diesen Kurs werden Grundlagen aus den anderen Kursen benötigt:

Lagebeziehungen

Überblick zu Lagebeziehungen im \(\mathbb{R}^3\).

Formen

$g:\; \vec{x} = \vec{p} + t\cdot\vec{d},\; t\in\mathbb{R}$

$E:\; \vec{x} = \vec{p} + s\cdot\vec{u} + t\cdot\vec{v},\; s,t\in\mathbb{R}\;\;\text{(Parameterform)}$

$E:\; (\vec{x}-\vec{p})\cdot\vec{n}=0\;\;\text{(Normalenform)}$

$E:\; n_1x_1+n_2x_2+n_3x_3=d\;\;\text{(Koordinatenform)}$

Lagebeziehung: Gerade-Gerade

Fälle: identisch · parallel · schneidend · windschief

Entscheidungsdiagramm

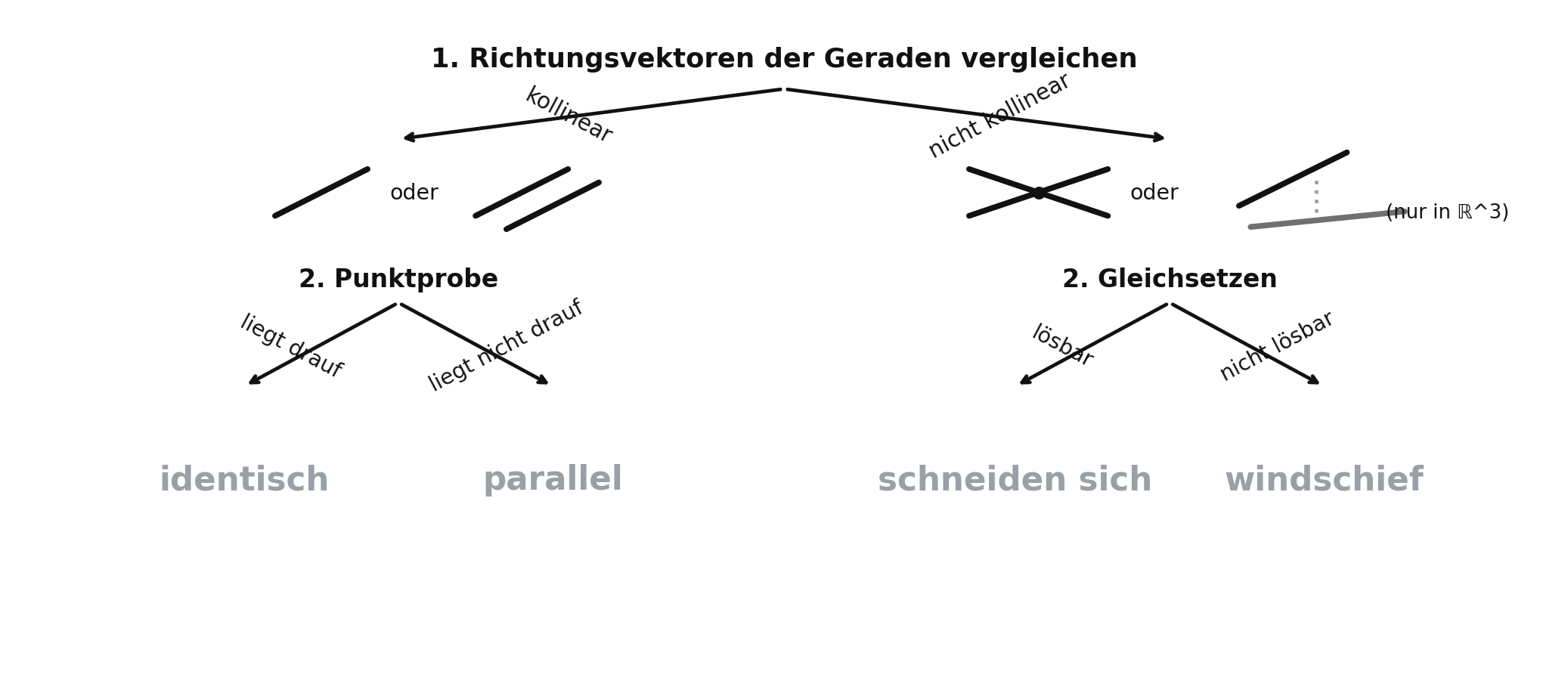
Entscheidungsdiagramm zur Lagebeziehung zweier Geraden

Geradengleichungen

$g:\; \vec{x}=\vec{a}+r\,\vec{u}\quad,\quad h:\; \vec{x}=\vec{b}+s\,\vec{v}$

Vorgehen

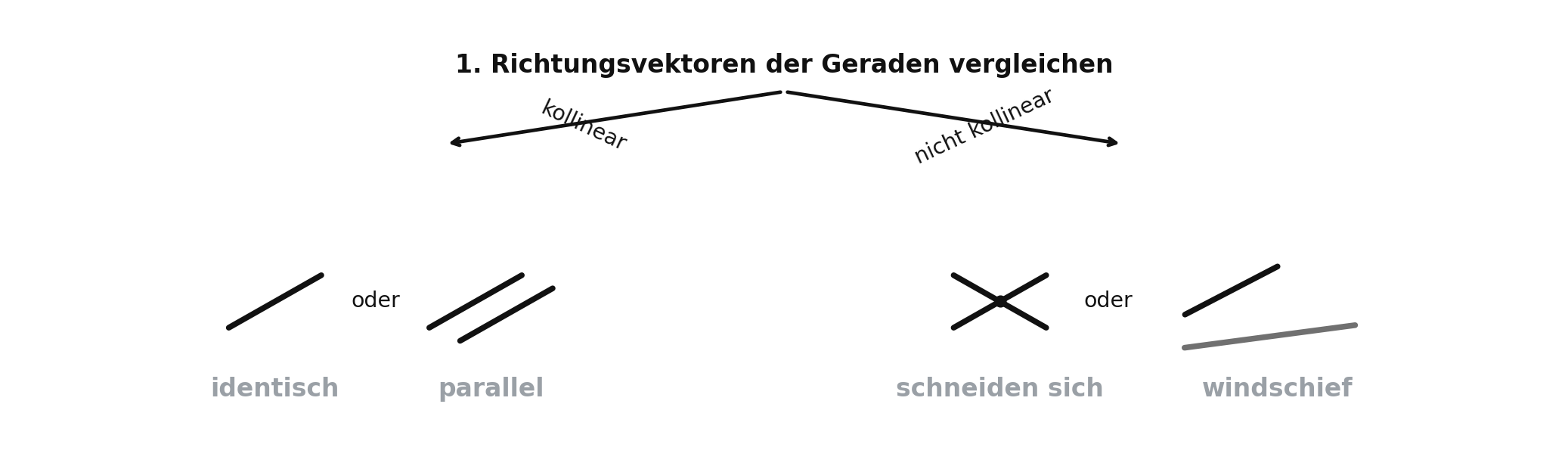
1) Richtungsvektoren vergleichen (Kollinearität / „Vielfache“):

  • Prüfe, ob \(\vec{u}\) und \(\vec{v}\) kollinear sind, d.h. ob es ein \(\lambda\in\mathbb{R}\) gibt mit \(\vec{u}=\lambda\,\vec{v}\) (oder umgekehrt).
  • Rechenweg: Ansatz \(\vec{u}=\lambda\,\vec{v}\) und komponentenweise prüfen.
  • Kollinearität Fallmenge: identisch oder parallel.
  • Nicht kollinear Fallmenge: schneidend oder (nur in \(\mathbb{R}^3\)) windschief.

$\vec{u}=\lambda\,\vec{v}\;\Longleftrightarrow\;\begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}=\lambda\begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix}\;\Longleftrightarrow\;\begin{cases}u_1=\lambda v_1\\u_2=\lambda v_2\\u_3=\lambda v_3\end{cases}$

Rechenweg (zeilenweise):

$\begin{aligned} u_1=\lambda v_1 &\Rightarrow \lambda=\dfrac{u_1}{v_1}\\ u_2=\lambda v_2 &\Rightarrow \lambda=\dfrac{u_2}{v_2}\\ u_3=\lambda v_3 &\Rightarrow \lambda=\dfrac{u_3}{v_3} \end{aligned}$

Kriterium: Wenn (wo definiert) in allen Zeilen derselbe Wert für \(\lambda\) herauskommt, sind die Richtungsvektoren Vielfache (kollinear).

Übersicht: Vielfache/nicht Vielfache und Beispiel-Skizzen

Ergebnis aus Schritt 1: Entweder kollinear dann sind nur identisch oder parallel möglich. Oder nicht kollinear dann sind nur schneiden sich oder windschief möglich. Schritt 2 dient der eindeutigen Zuordnung.

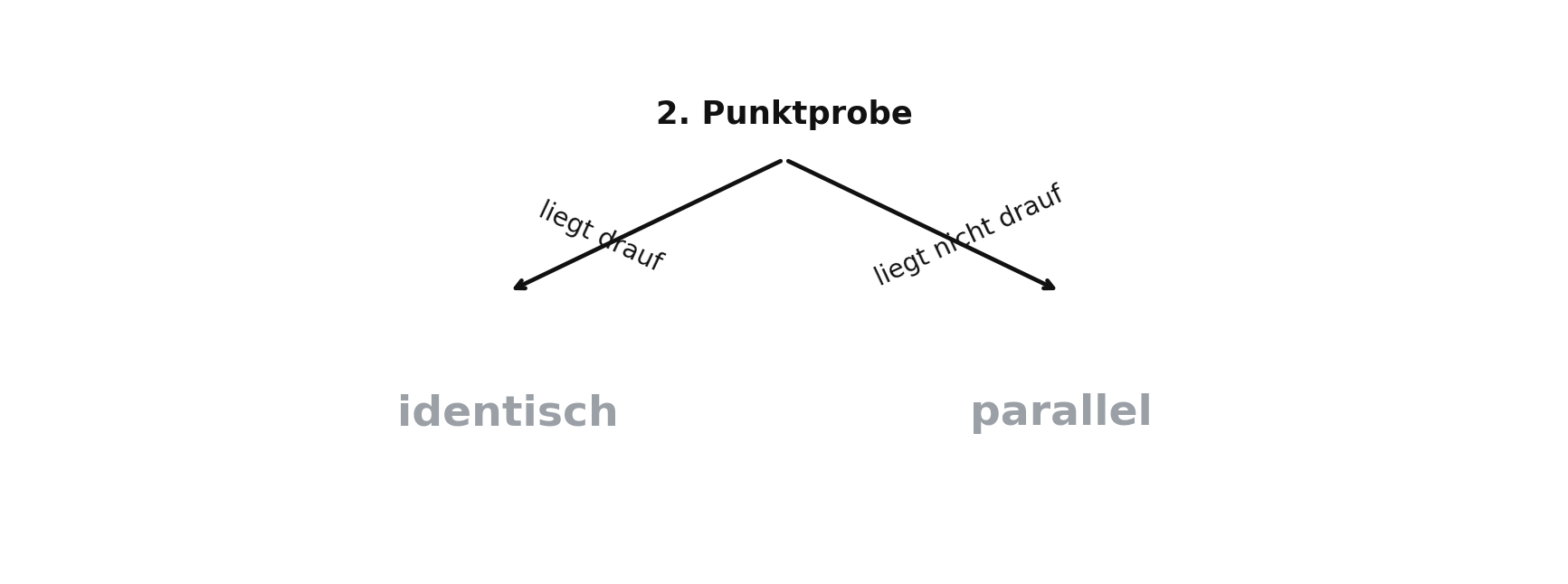
2a) Falls Vielfache (parallel/identisch): Punktprobe

  • Setze einen Stützpunkt (z.B. \(\vec{b}\) von \(h\)) in \(g\) ein: \(\vec{b}=\vec{a}+r\,\vec{u}\).
  • Ist das Gleichungssystem für \(r\) lösbar (konsistent), dann gilt \(\vec{b}\in g\) und die Geraden sind identisch.
  • Ist es nicht lösbar (widersprüchlich), dann gilt \(\vec{b}\notin g\) und die Geraden sind parallel.

$\vec{b}=\vec{a}+r\,\vec{u}\;\Longleftrightarrow\;\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}+r\begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}\;\Longleftrightarrow\;\begin{cases}b_1=a_1+r u_1\\b_2=a_2+r u_2\\b_3=a_3+r u_3\end{cases}$

Hinweis zur Auswertung: Bestimme \(r\) aus einer der drei Gleichungen (mit \(u_i\neq 0\)) und setze den Wert in die beiden übrigen Gleichungen ein. Sind alle drei Gleichungen erfüllt, ist die Punktprobe positiv (\(\vec{b}\in g\)).

Entscheidungsdiagramm: Punktprobe (kollinearer Fall)

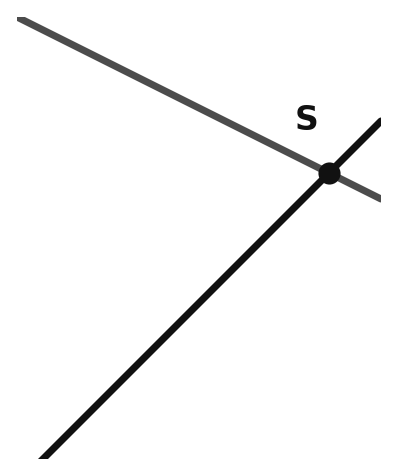
2b) Falls nicht Vielfache: Gleichsetzen (LGS)

  • Setze die Geraden gleich: \(\vec{a}+r\,\vec{u}=\vec{b}+s\,\vec{v}\) und löse das entstehende lineare Gleichungssystem nach \(r\) und \(s\).
  • Lösbar (konsistent): Es existiert ein gemeinsamer Punkt Geraden schneiden sich.
  • Nicht lösbar (widersprüchlich): Es existiert kein gemeinsamer Punkt Geraden sind windschief.
  • Im Schnittfall ergibt sich der Schnittpunkt durch Einsetzen, z.B. \(\vec{S}=\vec{a}+r\,\vec{u}\).

Rechenbeispiel: Entscheidung „schneidend oder windschief“

$g:\;\vec{x}=\begin{pmatrix}1\\0\\2\end{pmatrix}+r\begin{pmatrix}1\\2\\-1\end{pmatrix}\quad,\quad h:\;\vec{x}=\begin{pmatrix}2\\1\\1\end{pmatrix}+s\begin{pmatrix}2\\1\\1\end{pmatrix}$

Richtungsvektoren \(\begin{pmatrix}1\\2\\-1\end{pmatrix}\) und \(\begin{pmatrix}2\\1\\1\end{pmatrix}\) sind nicht kollinear also ist der Fall schneidend oder windschief.

1) Gleichsetzen und LGS aufstellen

$\begin{aligned} \begin{pmatrix}1\\0\\2\end{pmatrix}+r\begin{pmatrix}1\\2\\-1\end{pmatrix}&=\begin{pmatrix}2\\1\\1\end{pmatrix}+s\begin{pmatrix}2\\1\\1\end{pmatrix}\\ \Longleftrightarrow\quad\begin{cases} 1+r=2+2s\\ 2r=1+s\\ 2-r=1+s \end{cases} \end{aligned}$

2) Zwei Gleichungen lösen (Parameter bestimmen)

Aus Gleichung (2) und (3):

$\begin{aligned} 2r&=1+s\;\Rightarrow\;s=2r-1\\ 2-r&=1+s\;\Rightarrow\;s=1-r\\[4pt] 2r-1&=1-r\;\Rightarrow\;3r=2\;\Rightarrow\;r=\dfrac{2}{3}\\[4pt] s&=2r-1=2\cdot\dfrac{2}{3}-1=\dfrac{1}{3} \end{aligned}$

3) Konsistenzprüfung (dritte Gleichung testen)

Prüfe Gleichung (1) mit den gefundenen Werten:

$\begin{aligned} 1+r&\stackrel{?}{=}2+2s\\ 1+\dfrac{2}{3}&\stackrel{?}{=}2+2\cdot\dfrac{1}{3}\\ \dfrac{5}{3}&\neq\dfrac{8}{3} \end{aligned}$

Ergebnis: Widerspruch das LGS ist nicht lösbar die Geraden sind windschief.

Falls das LGS lösbar ist: Dann gilt schneiden sich und der Schnittpunkt kann berechnet werden durch Einsetzen der gefundenen Parameter.

Rechenbeispiel: Schnittpunkt berechnen (bei lösbarem LGS)

$g:\;\vec{x}=\begin{pmatrix}0\\1\\0\end{pmatrix}+r\begin{pmatrix}1\\0\\1\end{pmatrix}\quad,\quad h:\;\vec{x}=\begin{pmatrix}1\\0\\0\end{pmatrix}+s\begin{pmatrix}0\\1\\1\end{pmatrix}$

Gleichsetzen:

$\begin{aligned} \begin{pmatrix}0+r\\1\\0+r\end{pmatrix}&=\begin{pmatrix}1\\s\\s\end{pmatrix}\\ \Longleftrightarrow\quad\begin{cases} r=1\\ 1=s\\ r=s \end{cases} \end{aligned}$

$r=1\;\wedge\;s=1\quad\Rightarrow\quad \vec{S}=\vec{a}+r\,\vec{u}=\begin{pmatrix}0\\1\\0\end{pmatrix}+1\cdot\begin{pmatrix}1\\0\\1\end{pmatrix}=\begin{pmatrix}1\\1\\1\end{pmatrix}$

Die gefundenen Skalare (hier \(r=1\) und \(s=1\)) werden in die jeweilige Geradengleichung eingesetzt. Dadurch erhält man die Koordinaten des Schnittpunkts \(\vec{S}\). Zur Kontrolle kann \(\vec{S}\) auch mit der anderen Geraden berechnet werden (Einsetzen von \(s\)); es muss derselbe Punkt entstehen.

Skizze: Zwei Geraden schneiden sich im Punkt S

Entscheidungsdiagramm: 2. Gleichsetzen (lösbar/nicht lösbar)

Lagebeziehung: Gerade-Ebene

Fälle: Gerade liegt in Ebene · parallel · Schnittpunkt

Hinweis: Für die Entscheidung reicht ein Normalenvektor \(\vec{n}\) der Ebene und ein Ebenenpunkt \(\vec{p}\). Je nach gegebener Ebenenform kann eine geeignete Umformung (z.B. in Normalen- oder Koordinatenform) die Rechnung vereinfachen.

Formen:

$g:\; \vec{x}=\vec{a}+t\,\vec{u},\; t\in\mathbb{R}$

$E:\; (\vec{x}-\vec{p})\cdot\vec{n}=0\;\;\text{(Normalenform)}$

$E:\; ax+by+cz=d\;\;\text{(Koordinatenform)}$

$E:\; \vec{x}=\vec{p}+r\,\vec{v}+s\,\vec{w},\; r,s\in\mathbb{R}\;\;\text{(Parameterform)}$

Entscheidungsdiagramm

Normalenvektor bestimmen:

  • Koordinatenform \(ax+by+cz=d\): \(\vec{n}=\begin{pmatrix}a\\b\\c\end{pmatrix}\).
  • Normalenform \((\vec{x}-\vec{p})\cdot\vec{n}=0\): \(\vec{n}\) und \(\vec{p}\) sind direkt gegeben.
  • Parameterform \(\vec{x}=\vec{p}+r\vec{v}+s\vec{w}\): \(\vec{n}=\vec{v}\times\vec{w}\) und \(\vec{p}\) ist ein Ebenenpunkt.

Vorgehen:

$g:\; \vec{x}=\vec{a}+t\,\vec{u},\; t\in\mathbb{R}$

  • 1) Orthogonalitätsprüfung: Berechne \(\vec{u}\cdot\vec{n}\).
  • 2) Falls \(\vec{u}\cdot\vec{n}=0\): Gerade ist zur Ebene parallel. Führe eine Punktprobe mit \(\vec{a}\) durch:
    • Punktprobe erfüllt (z.B. \((\vec{a}-\vec{p})\cdot\vec{n}=0\)): Gerade liegt in der Ebene.
    • Mini-Beispiele zur Punktprobe (je nach Ebenenform):

      $\text{Koordinatenform: }E: x-y+2z=3,\;\vec{a}=\begin{pmatrix}1\\0\\1\end{pmatrix}$ $\Rightarrow\;1-0+2\cdot 1=3\;\checkmark\;\Rightarrow\;\vec{a}\in E$

      $\text{Normalenform: }E:(\vec{x}-\vec{p})\cdot\vec{n}=0,\;\vec{p}=\begin{pmatrix}1\\0\\1\end{pmatrix},\;\vec{n}=\begin{pmatrix}1\\-1\\2\end{pmatrix}$ $\vec{a}=\begin{pmatrix}3\\2\\2\end{pmatrix}\Rightarrow(\vec{a}-\vec{p})\cdot\vec{n}=\begin{pmatrix}2\\2\\1\end{pmatrix}\cdot\begin{pmatrix}1\\-1\\2\end{pmatrix}=2-2+2=0\;\checkmark$

      $\text{Parameterform: }E:\;\vec{x}=\begin{pmatrix}1\\0\\1\end{pmatrix}+r\begin{pmatrix}1\\0\\1\end{pmatrix}+s\begin{pmatrix}0\\1\\0\end{pmatrix},\;\vec{a}=\begin{pmatrix}3\\2\\3\end{pmatrix}$ $\Rightarrow\;\begin{pmatrix}3\\2\\3\end{pmatrix}=\begin{pmatrix}1+r\\s\\1+r\end{pmatrix}\Rightarrow r=2,\;s=2\Rightarrow\vec{a}\in E$

    • Punktprobe nicht erfüllt: Gerade ist parallel zur Ebene (kein Schnittpunkt).
  • 3) Falls \(\vec{u}\cdot\vec{n}\neq 0\): Es gibt genau einen Schnittpunkt. Berechne den Parameter \(t\) und anschließend \(\vec{S}=\vec{a}+t\vec{u}\).

Ergebnis: Gerade liegt in der Ebene \(\Leftrightarrow\; \vec{u}\cdot\vec{n}=0\) und die Punktprobe ist erfüllt (z.B. \((\vec{a}-\vec{p})\cdot\vec{n}=0\)).

Ergebnis: Gerade ist parallel zur Ebene \(\Leftrightarrow\; \vec{u}\cdot\vec{n}=0\) und die Punktprobe ist nicht erfüllt.

Ergebnis: Gerade schneidet die Ebene \(\Leftrightarrow\; \vec{u}\cdot\vec{n}\neq 0\). In diesem Fall ist der Schnittpunkt \(\vec{S}=\vec{a}+t\vec{u}\) eindeutig.

Beispielrechnung (Schnittpunkt, Koordinatenform):

$E:\;x-2y+z=3\qquad g:\;\vec{x}=\begin{pmatrix}1\\0\\0\end{pmatrix}+t\begin{pmatrix}1\\1\\0\end{pmatrix}$

$\vec{n}=\begin{pmatrix}1\\-2\\1\end{pmatrix}\;\Rightarrow\;\vec{n}\cdot\vec{u}=\begin{pmatrix}1\\-2\\1\end{pmatrix}\cdot\begin{pmatrix}1\\1\\0\end{pmatrix}=-1\neq 0$

$g:\;x=1+t,\;y=t,\;z=0\;\Rightarrow\;(1+t)-2t+0=3\;\Rightarrow\;t=-2$

$\vec{S}=\begin{pmatrix}1\\0\\0\end{pmatrix}+(-2)\begin{pmatrix}1\\1\\0\end{pmatrix}=\begin{pmatrix}-1\\-2\\0\end{pmatrix}$

Beispielrechnung (Schnittpunkt, Normalenform):

$E:(\vec{x}-\vec{p})\cdot\vec{n}=0,\;\vec{p}=\begin{pmatrix}0\\1\\2\end{pmatrix},\;\vec{n}=\begin{pmatrix}2\\-1\\1\end{pmatrix}$

$g:\;\vec{x}=\vec{a}+t\vec{u},\;\vec{a}=\begin{pmatrix}1\\0\\0\end{pmatrix},\;\vec{u}=\begin{pmatrix}1\\2\\1\end{pmatrix}$

$\vec{n}\cdot\vec{u}=\begin{pmatrix}2\\-1\\1\end{pmatrix}\cdot\begin{pmatrix}1\\2\\1\end{pmatrix}=2-2+1=1\neq 0$

1) Einsetzen der Geraden in die Normalenform

$E:(\vec{x}-\vec{p})\cdot\vec{n}=0\quad\text{und}\quad g:\vec{x}=\vec{a}+t\vec{u}$ $\Rightarrow\;((\vec{a}+t\vec{u})-\vec{p})\cdot\vec{n}=0$

2) Ausmultiplizieren und nach \(t\) lösen

$((\vec{a}-\vec{p})+t\vec{u})\cdot\vec{n}=0$ $(\vec{a}-\vec{p})\cdot\vec{n}+t(\vec{u}\cdot\vec{n})=0$ $\Rightarrow\;t=-\dfrac{(\vec{a}-\vec{p})\cdot\vec{n}}{\vec{u}\cdot\vec{n}}=\dfrac{\vec{n}\cdot(\vec{p}-\vec{a})}{\vec{n}\cdot\vec{u}}$

$\vec{p}-\vec{a}=\begin{pmatrix}0\\1\\2\end{pmatrix}-\begin{pmatrix}1\\0\\0\end{pmatrix}=\begin{pmatrix}-1\\1\\2\end{pmatrix}$ $\vec{n}\cdot(\vec{p}-\vec{a})=\begin{pmatrix}2\\-1\\1\end{pmatrix}\cdot\begin{pmatrix}-1\\1\\2\end{pmatrix}=-2-1+2=-1$ $\vec{n}\cdot\vec{u}=1\Rightarrow\;t=\dfrac{-1}{1}=-1$

3) Schnittpunkt berechnen (\(t\) in die Gerade einsetzen)

$\vec{S}=\vec{a}+t\vec{u}=\begin{pmatrix}1\\0\\0\end{pmatrix}+(-1)\begin{pmatrix}1\\2\\1\end{pmatrix}=\begin{pmatrix}0\\-2\\-1\end{pmatrix}$

Beispielrechnung (Schnittpunkt, Parameterform):

$E:\;\vec{x}=\vec{p}+r\vec{v}+s\vec{w},\;\vec{p}=\begin{pmatrix}1\\0\\1\end{pmatrix},\;\vec{v}=\begin{pmatrix}1\\1\\0\end{pmatrix},\;\vec{w}=\begin{pmatrix}2\\-1\\1\end{pmatrix}$

$g:\;\vec{x}=\vec{a}+t\vec{u},\;\vec{a}=\begin{pmatrix}0\\2\\3\end{pmatrix},\;\vec{u}=\begin{pmatrix}1\\-1\\2\end{pmatrix}$

$\vec{a}+t\vec{u}=\vec{p}+r\vec{v}+s\vec{w}$ $\begin{pmatrix}0\\2\\3\end{pmatrix}+t\begin{pmatrix}1\\-1\\2\end{pmatrix}=\begin{pmatrix}1\\0\\1\end{pmatrix}+r\begin{pmatrix}1\\1\\0\end{pmatrix}+s\begin{pmatrix}2\\-1\\1\end{pmatrix}$

$\Rightarrow\;\begin{cases} t=1+r+2s\\ 2-t=r-s\\ 3+2t=1+s \end{cases}$

$\text{Aus (3): }\;s=2+2t$

$\text{In (1): }\;t=1+r+2s=1+r+2(2+2t)\Rightarrow r=-3t-5$

$\text{In (2): }\;2-t=r-s=(-3t-5)-(2+2t)=-5t-7\Rightarrow 4t=-9\Rightarrow t=-\dfrac{9}{4}$

$\Rightarrow\;s=2+2t=-\dfrac{5}{2},\;r=-3t-5=\dfrac{7}{4}$

$\vec{S}=\vec{a}+t\vec{u}=\begin{pmatrix}0\\2\\3\end{pmatrix}+\left(-\dfrac{9}{4}\right)\begin{pmatrix}1\\-1\\2\end{pmatrix}=\begin{pmatrix}-\dfrac{9}{4}\\\dfrac{17}{4}\\-\dfrac{3}{2}\end{pmatrix}$

Lagebeziehung: Ebene-Ebene

Fälle: identisch · parallel · Schnittgerade

Entscheidungsdiagramm

1) Normalen vergleichen

Prüfen: \(\vec{n}_1 \parallel \vec{n}_2\)? (\(\vec{n}_1=\lambda\,\vec{n}_2\)?)

Voraussetzung: Bestimme für jede Ebene einen Normalenvektor \(\vec{n}\).

  • Koordinatenform: \(E: ax+by+cz=d\) \(\Rightarrow\) \(\vec{n}=\begin{pmatrix}a\\b\\c\end{pmatrix}\) (direkt ablesbar)
  • Normalenform: \(E:(\vec{x}-\vec{p})\cdot\vec{n}=0\) \(\Rightarrow\) \(\vec{n}\) ist direkt gegeben
  • Parameterform: \(E:\vec{x}=\vec{p}+s\,\vec{u}+t\,\vec{v}\) \(\Rightarrow\) \(\vec{n}=\vec{u}\times\vec{v}\)

Schritt 1: Kollinearität prüfen

$\vec{n}_1=\lambda\,\vec{n}_2\;?\;\; (\lambda\in\mathbb{R})$

Mini-Beispiel (Kollinearität der Normalen):

$\vec{n}_1=\begin{pmatrix}2\\-1\\3\end{pmatrix},\;\vec{n}_2=\begin{pmatrix}-4\\2\\-6\end{pmatrix}$ $\vec{n}_1=\lambda\,\vec{n}_2\;\Rightarrow\;\begin{cases} 2=\lambda\cdot(-4)\\ -1=\lambda\cdot 2\\ 3=\lambda\cdot(-6) \end{cases}$ $2=\lambda\cdot(-4)\Rightarrow \lambda=-\dfrac{1}{2}$ $\text{Probe: }\; -1=(-\tfrac{1}{2})\cdot 2\;\checkmark\;\;\;3=(-\tfrac{1}{2})\cdot(-6)\;\checkmark$ $\Rightarrow\;\vec{n}_1\parallel\vec{n}_2\;\text{(kollinear)}\;\Rightarrow\;\text{Ebenen sind parallel oder identisch (Punktprobe).}$

  • Fall \(\vec{n}_1\not\parallel\vec{n}_2\): \(\Rightarrow\) Die Ebenen schneiden sich; die Schnittmenge ist eine Schnittgerade. Bestimme die Schnittgerade durch Lösen des Gleichungssystems.
  • Fall \(\vec{n}_1\parallel\vec{n}_2\): \(\Rightarrow\) Führe eine Punktprobe durch: Prüfe, ob ein Punkt \(\vec{p}_1\in E_1\) auch in \(E_2\) liegt.

Punktprobe (bei \(\vec{n}_1\parallel\vec{n}_2\)): Setze einen Punkt \(\vec{p}_1\in E_1\) in die Gleichung von \(E_2\) ein.

  • Punktprobe erfüllt: \(\vec{p}_1\in E_2\) \(\Rightarrow\) Ebenen sind identisch.
  • Punktprobe nicht erfüllt: \(\vec{p}_1\notin E_2\) \(\Rightarrow\) Ebenen sind parallel (verschieden, kein Schnitt).

2) Punktprobe

  • 1) Wähle einen Punkt \(\vec{p}_1\) aus \(E_1\):
    • Koordinatenform \(ax+by+cz=d\): Setze zwei Variablen frei (zum Beispiel \(y=0\), \(z=0\)) und berechne die dritte.
    • Normalenform \((\vec{x}-\vec{p})\cdot\vec{n}=0\): Der Stützpunkt \(\vec{p}\) liegt auf der Ebene, also \(\vec{p}_1=\vec{p}\).
    • Parameterform \(\vec{x}=\vec{p}+s\vec{u}+t\vec{v}\): Setze z.B. \(s=0\), \(t=0\) dann ist \(\vec{p}_1=\vec{p}\).
  • 2) Setze \(\vec{p}_1\) in \(E_2\) ein:
    • Wenn \(E_2\) in Koordinatenform vorliegt: Prüfe \(\vec{n}_2\cdot\vec{p}_1\stackrel{?}{=}d_2\).
    • Wenn \(E_2\) in Normalenform vorliegt: Prüfe \((\vec{p}_1-\vec{p}_2)\cdot\vec{n}_2\stackrel{?}{=}0\).
    • Wenn \(E_2\) in Parameterform vorliegt: Setze \(\vec{p}_1=\vec{p}+s\vec{u}+t\vec{v}\) an und löse das entstehende lineare Gleichungssystem nach \(s\) und \(t\).
      • Lösbar: \(\vec{p}_1\in E_2\) (Punktprobe positiv)
      • Nicht lösbar: \(\vec{p}_1\notin E_2\) (Punktprobe negativ)

Beispielrechnung (Punktprobe, wenn \(E_2\) in Parameterform gegeben ist)

Gegeben:

$E_2:\; \vec{x}=\begin{pmatrix}1\\0\\2\end{pmatrix}+s\begin{pmatrix}1\\1\\1\end{pmatrix}+t\begin{pmatrix}2\\-1\\1\end{pmatrix}$

$\vec{p}_1=\begin{pmatrix}3\\4\\3\end{pmatrix}$

1) Ansatz (Gleichungssystem): \(\vec{p}_1=\vec{p}+s\vec{u}+t\vec{v}\)

$\begin{pmatrix}3\\4\\3\end{pmatrix}=\begin{pmatrix}1\\0\\2\end{pmatrix}+s\begin{pmatrix}1\\1\\1\end{pmatrix}+t\begin{pmatrix}2\\-1\\1\end{pmatrix}$

2) Komponentenvergleich:

$\begin{cases} 3=1+s+2t\\ 4=s-t\\ 3=2+s+t \end{cases}$

3) Lösen und prüfen:

Es werden beispielsweise die ersten beiden Gleichungen nach \(s\) und \(t\) gelöst und anschließend mit der dritten Gleichung geprüft:

$\begin{aligned} 4&=s-t\Rightarrow s=4+t\\ 3&=1+s+2t\Rightarrow 2=s+2t \end{aligned}$

$2=(4+t)+2t\Rightarrow 4+3t=2\Rightarrow t=-\dfrac{2}{3}\Rightarrow s=4-\dfrac{2}{3}=\dfrac{10}{3}$

$\text{Kontrolle in der 3. Gleichung:}\;3\stackrel{?}{=}2+s+t=2+\dfrac{10}{3}-\dfrac{2}{3}=\dfrac{14}{3}\;\Rightarrow\;\text{Widerspruch}$

Ergebnis: Das Gleichungssystem ist nicht lösbar \(\Rightarrow\) \(\vec{p}_1\notin E_2\) (Punktprobe negativ).

Interpretation (Punktprobe bei Parameterform als Gleichungssystem):

  • Gleichungssystem lösbar: Es existieren Werte \(s,t\) mit \(\vec{p}_1=\vec{p}+s\vec{u}+t\vec{v}\). Dann gilt \(\vec{p}_1\in E_2\) \(\Rightarrow\) (bei \(\vec{n}_1\parallel\vec{n}_2\)) Ebenen identisch.
  • Gleichungssystem nicht lösbar: Es existieren keine Werte \(s,t\), die alle drei Komponentengleichungen erfüllen. Dann gilt \(\vec{p}_1\notin E_2\) \(\Rightarrow\) (bei \(\vec{n}_1\parallel\vec{n}_2\)) Ebenen parallel (verschieden).

Zusatzfall: Ebenen schneiden sich (Schnittgerade)

Wenn \(\vec{n}_1\not\parallel\vec{n}_2\) gilt, dann ist die Schnittmenge von \(E_1\) und \(E_2\) eine Gerade (Schnittgerade).

Allgemeines Vorgehen (Schnittgerade bestimmen):

  • 1) Beide Ebenen in Koordinatenform bringen (wenn nötig): \(a x+b y+c z=d\).
    • Koordinatenform: schon fertig.
    • Normalenform \((\vec{x}-\vec{p})\cdot\vec{n}=0\): \(\vec{n}=(a,b,c)^T\) und \(d=\vec{n}\cdot\vec{p}\).
    • Parameterform \(\vec{x}=\vec{p}+s\vec{u}+t\vec{v}\): \(\vec{n}=\vec{u}\times\vec{v}\) und \(d=\vec{n}\cdot\vec{p}\) \(\Rightarrow\) Koordinatenform \(\vec{n}\cdot\vec{x}=d\).
  • 2) Gleichungssystem aufstellen: Löse \(\begin{cases}a_1x+b_1y+c_1z=d_1\\a_2x+b_2y+c_2z=d_2\end{cases}\) mit drei Unbekannten.
  • 3) Eine Variable frei wählen (Parameter), z.B. \(z=t\), und die beiden verbleibenden Unbekannten aus den zwei Gleichungen berechnen.
  • 4) Schnittgerade angeben: Schreibe die Lösung als Parameterdarstellung \(g:\;\vec{x}=\vec{x}_0+t\,\vec{d}\). Dabei ist \(\vec{x}_0\) ein konkreter Schnittpunkt und \(\vec{d}\) ein Richtungsvektor. (Optional: \(\vec{d}=\vec{n}_1\times\vec{n}_2\) liefert direkt eine Richtung der Schnittgeraden.)

Beispielrechenweg (Schnittgerade über Gleichungssystem)

Gegeben (Koordinatenform):

$E_1:\;2x-y+3z=7\qquad E_2:\;-x+4y+z=5$

2) Gleichungssystem aufstellen:

$\begin{cases} 2x-y+3z=7\\ -x+4y+z=5 \end{cases}$

3) Eine Variable frei wählen (Parameter): Setze \(z=t\).

$\begin{cases} 2x-y=7-3t\\ -x+4y=5-t \end{cases}$

Lösen: Zuerst \(y\) aus der ersten Gleichung ausdrücken und in die zweite einsetzen.

$2x-y=7-3t\Rightarrow y=2x-7+3t$

$-x+4(2x-7+3t)=5-t\Rightarrow 7x=33-13t\Rightarrow x=\dfrac{33-13t}{7}$

$y=2x-7+3t=2\cdot\dfrac{33-13t}{7}-7+3t=\dfrac{17-5t}{7}$

4) Schnittgerade angeben: Zusammen mit \(z=t\):

$g:\;\vec{x}=\begin{pmatrix}\dfrac{33-13t}{7}\\\dfrac{17-5t}{7}\\t\end{pmatrix}=\begin{pmatrix}\dfrac{33}{7}\\\dfrac{17}{7}\\0\end{pmatrix}+t\begin{pmatrix}-\dfrac{13}{7}\\-\dfrac{5}{7}\\1\end{pmatrix}$

Hier ist \(\vec{x}_0=\begin{pmatrix}\dfrac{33}{7}\\\dfrac{17}{7}\\0\end{pmatrix}\) ein Punkt auf der Schnittgeraden. Der Richtungsvektor ergibt sich direkt aus den \(t\)-Koeffizienten:

$\vec{d}=\begin{pmatrix}-\dfrac{13}{7}\\-\dfrac{5}{7}\\1\end{pmatrix}\sim\begin{pmatrix}-13\\-5\\7\end{pmatrix}$

Optionaler Check (Richtung über Kreuzprodukt):

Dieser Check liefert einen Richtungsvektor der Schnittgeraden (ohne das Gleichungssystem vollständig zu lösen) und dient als Plausibilitätskontrolle: Der Vektor \(\vec{n}_1\times\vec{n}_2\) muss (bis auf einen Skalarfaktor) parallel zum aus der Rechnung bestimmten \(\vec{d}\) sein.

$\vec{n}_1=\begin{pmatrix}2\\-1\\3\end{pmatrix},\;\vec{n}_2=\begin{pmatrix}-1\\4\\1\end{pmatrix}\Rightarrow \vec{n}_1\times\vec{n}_2=\begin{pmatrix}-13\\-5\\7\end{pmatrix}$

↑ ↑ ↑